Puoluekannatus ja virhemarginaalit

Alma Media ja Yle julkistivat joulukuun lopulla peräkkäisinä päivinä puolueiden kuntavaalikannatusta koskevat mielipidemittauksensa. Tietoykkönen Oy:n Almalle toteuttaman kyselyn haastattelut tehtiin 9.–18.12., Taloustutkimus taas toteutti Ylen kyselyn 7.–28.12. Puolueiden kannatusprosentit kummassakin kyselyssä on lueteltu alla olevassa taulukossa.

	Yle	Alma Media
SDP	21,2 %	20,1 %
keskusta	20,3 %	19,5 %
kokoomus	17,4 %	17,1 %
vihreät	13,3 %	11,2 %
PS	9,4 %	11,6 %
vasemmistoliitto	7,6 %	8,8 %
RKP	4,9 %	4,5 %
KD	3,6 %	3,7 %
muut	2,3 %	3,5 %

Puolueiden kannatuksissa on havaittavissa pieniä eroja kyselyiden välillä. Huolimatta siitä, että mielipidemittausten aikavälit poikkeavat hieman toisistaan, Alman kyselyn aikaväli mahtuu kokonaan Ylen kyselyn ”sisään”. Voisi kuvitella, että liki samaan aikaan tehdyt mielipidemittaukset antaisivat melko tarkalleen samat kannatuslukemat kullekin puolueelle. Näin ei kuitenkaan ole. Mistä se johtuu?

Vastaus kysymykseen löytyy tietenkin mielipidemittausten virhemarginaalista. Mutta mitä virhemarginaali oikeastaan tarkoittaa ja miten sitä pitäisi tulkita?

Virhemarginaali ja luottamusväli

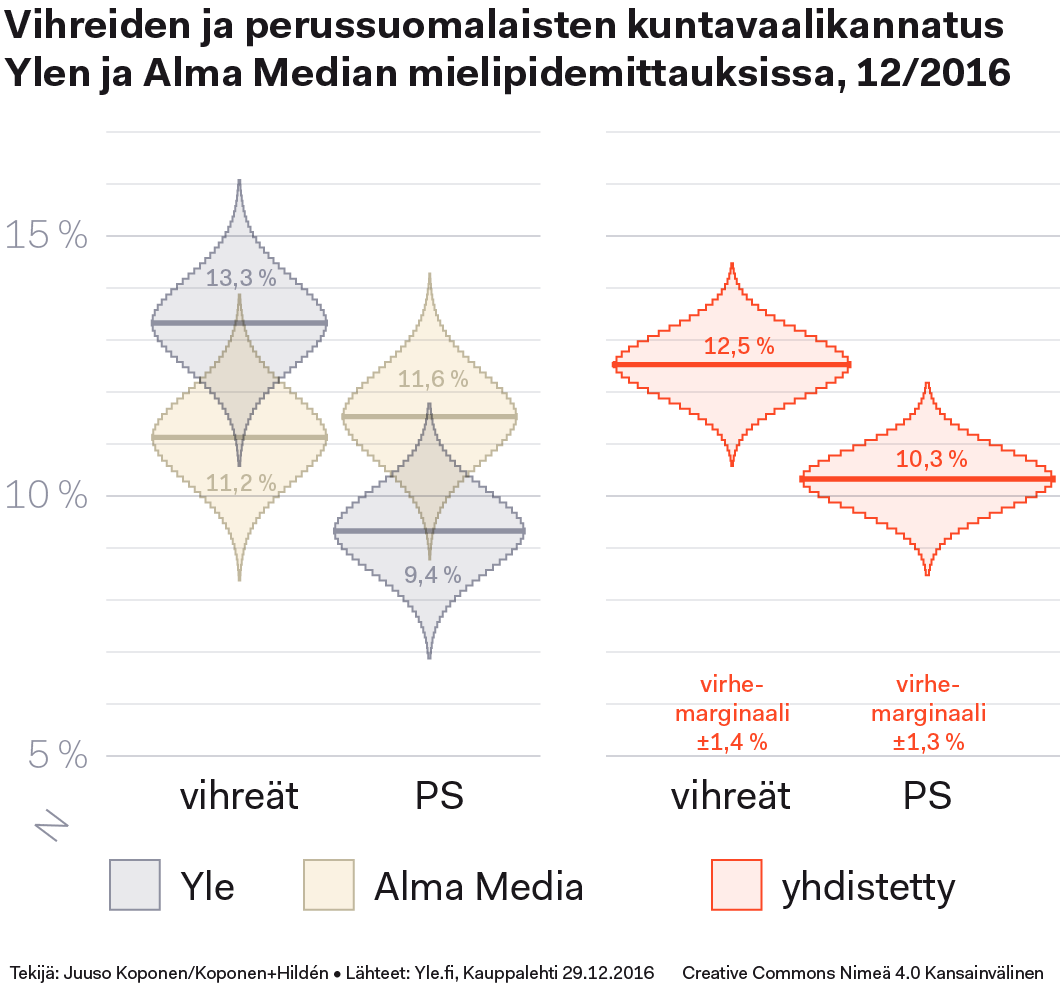
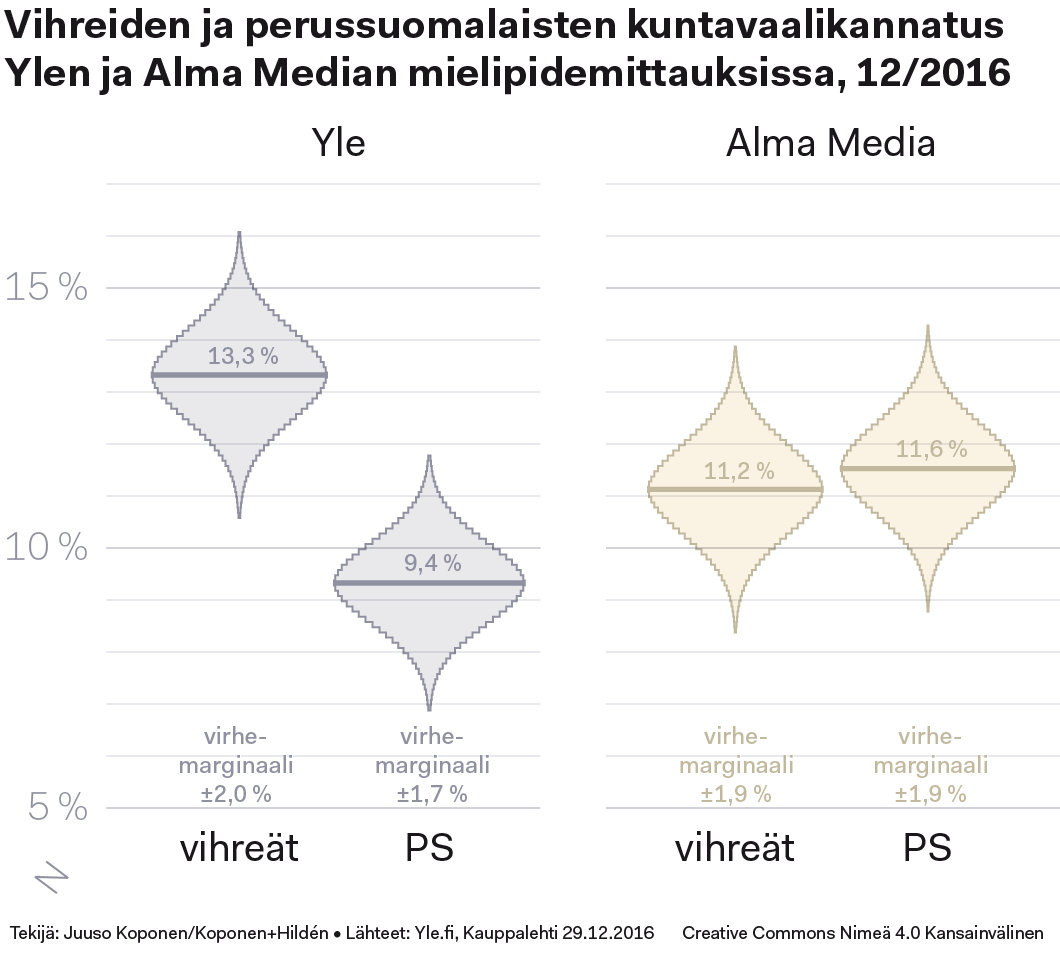
Otetaan lähempään tarkasteluun ne kaksi puoluetta, joiden kannatuslukemissa ero Ylen ja Alma Median kyselyiden välillä on suurin: poliittisen spektrin vastakkaisilta laidoilta löytyvät vihreät ja perussuomalaiset.

Ylen kyselyssä vihreät on neljänneksi suurin puolue selvällä erolla viidenneksi suurimpaan puolueeseen perussuomalaisiin. Alma Median kyselyssä puolueet taas ovat lähes tasoissa, mutta perussuomalaiset johtaa vihreitä täpärästi.

Molempien kyselyiden ilmoitettu virhemarginaali on ±2,4 prosenttiyksikköä. Tarkoittaako tämä, että esimerkiksi vihreiden todellinen kannatus voi Ylen kyselyn mukaan olla yhtä hyvin mikä hyvänsä luku välillä 10,9–15,7 % ja Alma Median mukaan välillä 8,8–13,6 %? Ei tarkoita.

Ensin lienee hyvä hieman avata, mikä on virhemarginaalin määritelmä. Tilastotieteellisin termein ilmaistuna mielipidemittauksen virhemarginaali on sama asia kuin 95 prosentin luottamusvälin (engl. confidence interval) puolikas. Tämä tarkoittaa siis sitä, että mikäli tutkimuksen otos on harhaton (tästä lisää artikkelin loppupuolella) puolueen todellinen kannatus on 95 prosentin todennäköisyydellä jollain kohtaa vaihteluväliä, joka ulottuu virhemarginaalin verran ilmoitetusta prosenttiluvusta kumpaankin suuntaan.

Kyselyn virhemarginaali lasketaan seuraavalla kaavalla:

Kaavassa p merkitsee puoluekannatuksen tai muun mittauksen kohteena olevan asian suhteellista osuutta desimaalilukuna (esim. vihreiden kannatus Ylen kyselyssä = 0,133) ja n kyselyyn vastanneiden määrää eli otoskokoa. 1,96 tulee kaavaan taas siitä, että 95 prosentin vaihteluvälin äärirajat ovat ±1,96 keskihajonnan etäisyydellä keskiarvosta.

Suoraan kaavasta ilmenee kaksi merkittävää virhemarginaalia koskevaa seikkaa:

1. Populaation eli perusjoukon, siis koko tutkimuksen kohteena olevan ryhmän koko ei vaikuta virhemarginaaliin. Voi tuntua epäintuitiiviselta, että puolueiden kannatuksen selvittämiseksi koko Suomessa (5,5 milj. as.) tai pelkästään vaikkapa Lappeenrannassa (73 000 as.) tarvitaan yhtä suuri otos saman virhemarginaalin saamiseksi. Mikäli otoskoko on hyvin lähellä populaation kokoa, näin ei itse asiassa olekaan, mutta useimmissa käytännön tilanteissa sama otos tuottaa mielipidemittauksessa yhtä suuren virhemarginaalin, oli tutkimuksen kohteena sitten 50 miljoonan tai 50 000:n kokoinen ihmisjoukko.
    
2. Erisuuruisilla kannatusluvuilla on eri virhemarginaalit. Tämä merkitsee sitä, että mielipidemittauksen ilmoitettu virhemarginaali pätee sellaisenaan vain yhteen vertailussa mukana olevista puolueista (yleensä suurimpaan niistä). Luvun virhemarginaali on sitä suurempi, mitä lähempänä 50 prosenttia se on. Niinpä pienempien puolueiden kohdalla todellinen marginaali on ilmoitettua pienempi.

Ylen kyselyyn vastasi 1 946 henkilöä, joista 57,6 % eli 1 121 kertoi puoluekantansa. Alma Mediaa varten haastatelluista 1 500 henkilöstä kantansa ilmaisi 70,8 % eli 1 062. Näillä luvuilla saadaan yllä esitettyä kaavaa käyttäen laskettua seuraavat virhemarginaalit kullekin puolueelle:

	Yle (n = 1 121)	Alma Media (n = 1 062)
SDP	±2,4 %	±2,4 %
keskusta	±2,4 %	±2,4 %
kokoomus	±2,2 %	±2,3 %
vihreät	±2,0 %	±1,9 %
PS	±1,7 %	±1,9 %
vasemmistoliitto	±1,6 %	±1,7 %
RKP	±1,3 %	±1,2 %
KD	±1,1 %	±1,1 %
muut	±0,9 %	±1,1 %

Todellinen arvo voi olla myös virhemarginaalin ulkopuolella

On huomionarvoista, että virhemarginaalin laskemiseen käytetty luottamusväli on 95, ei suinkaan 100 prosenttia. Todellinen arvo voi siis löytyä myös virhemarginaalin ulkopuoleltakin. Yksittäisen puolueen kannatuksen tapauksessa tämän todennäköisyys on vain 5 %, mutta koska yhdestä mielipidemittauksesta ilmenee 9 eri numeroa  – 8 puolueen kannatusprosentit sekä ryhmä ”muut” – todennäköisyys sille, että ainakin yksi niistä on pielessä virhemarginaalia enemmän on 37 %. Todennäköisyys sille, että ainakin yksi joko Ylen tai Alma Median luvuista on virhemarginaalia kauempana todellisuudesta on jo 60 %, ja on lähestulkoon varmaa (todennäköisyys 99,6 %), että ainakin yksi Ylen vuoden aikana julkaisemista 12 mielipidemittauksista sisältää vähintään yhden kannatuslukeman, jonka todellinen arvo on virhemarginaalin ulkopuolella.

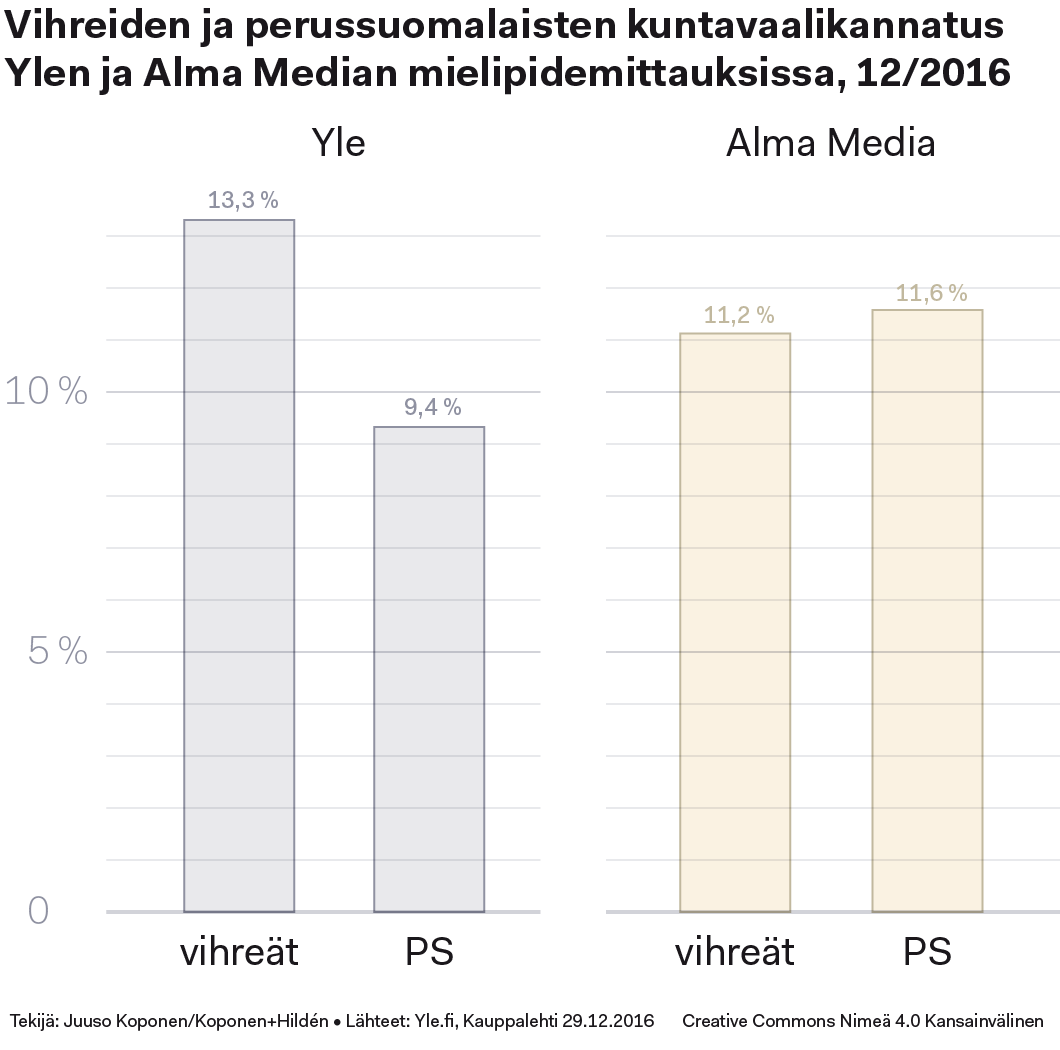
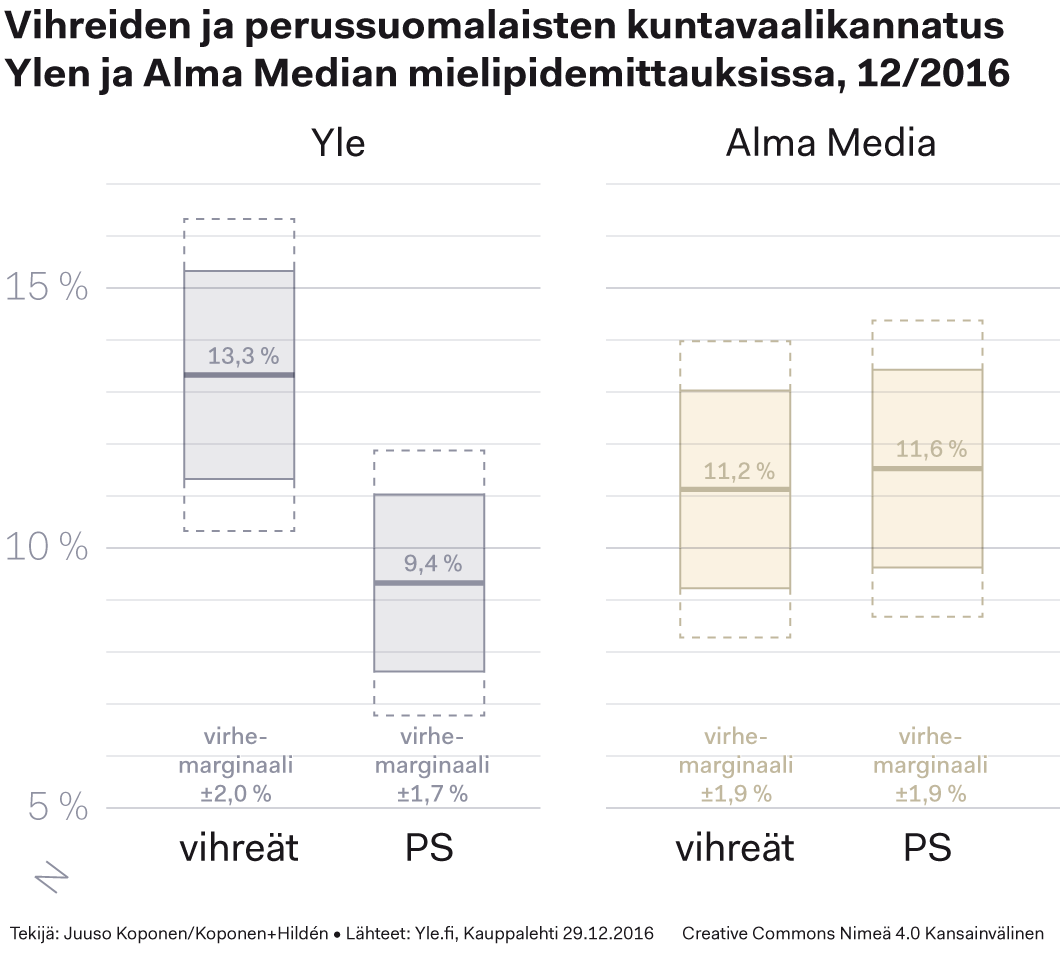
Yllä olevassa kuviossa on kuvattu se vaihteluväli jolle vihreiden ja perussuomalaisten todellinen kannatus Ylen ja Alma Median kannatusmittausten mukaan sijoittuu. Tavallinen, 95 prosentin luottamusväliin perustuva virhemarginaali on kuvattu täytettynä laatikkona, lisäksi katkoviivalla on osoitettu 99,7 prosentin luottamusväli (±3,0 keskihajontaa), jonka sisältä oikea arvo löytyy jo lähes varmasti.

Parikin prosenttiyksikköä on aika iso heitto kun puhutaan kymmenen prosentin tietämissä pyörivistä luvuista. Kuten ylempänä kuvatusta laskukaavasta ilmenee, virhemarginaalia olisi mahdollista pienentää otoskokoa kasvattamalla. Miksi näin ei tehdä mielipidemittausten tulosten tarkentamiseksi? Syy on yksinkertainen: raha. Virhemarginaalin puolittaminen vaatisi otoskoon nelinkertaistamista ja kustannukset kasvaisivat samassa suhteessa. Noin tuhannen vastaajan otos on vuosikymmenten saatossa päätetty tarkkuudeltaan median käyttöön riittäväksi kun otetaan huomioon myös mittausten teettämisen kustannus.

Lisäksi on syytä huomioida, että kaikki arvot virhemarginaalin sisällä eivät ole yhtä todennäköisiä. Virhemarginaalin olessa ±2,0 prosenttiyksikköä todellinen arvo on 68 prosentin todennäköisyydellä korkeintaan yhden prosenttiyksikön päässä keskiarvosta.

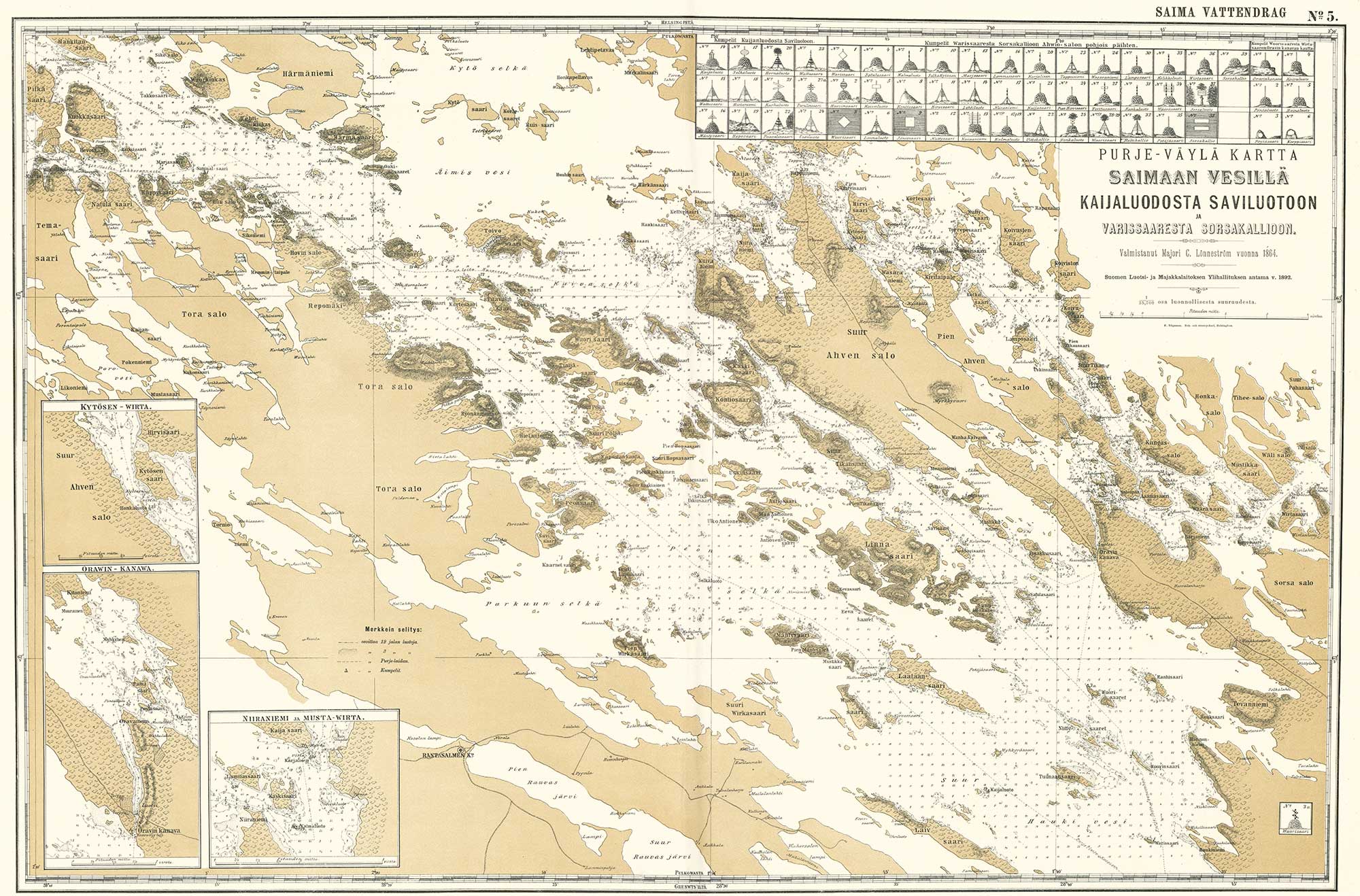
Alla oleva kuvio esittää vihreiden ja perussuomalaisten kannatuslukujen todennäköisyysjakauman. Todennäköisyys sille, että todellinen kannatusluku osuu kuvion keskellä olevalle tummennetulle alueelle on kussakin tapauksessa n. 4 % ja pienenee siitä etäännyttäessä. Kuvioelementtien kärjet kuvaavat 99,7 prosentin luottamusväliä.

Tämäkään kuvio ei silti vielä anna kovin hyvää vastausta siihen, mikä puolueiden todellinen kannatus on. Ylen yhden puolueen kannatukselle antama, kuviossa tummennettu todennäköisin arvo on aivan Alma Median todennäköisyysjakauman äärilaidalla ja päinvastoin.

Useamman mielipidemittauksen tulosten yhdistäminen

Usein tarkin tulos saadaan kun kahden tai useamman mielipidemittausten sisältämä tieto yhdistetään ja muodostetaan aineistosta uusi kuvio. Tähän on olemassa erilaisia tapoja. Maailmalla toimii useita mielipidemittausten tulosten yhdistelyyn erikoistuneita verkkosivustoja, joita kutsutaan mielipideaggregaattoreiksi (engl. poll aggregator). Ne ovat kehittäneet monimutkaisia, erilaisia paino- ja korjauskertoimia hyödyntäviä menetelmiään tarkoitukseen. Tunnetuin aggregaattoreista lienee FiveThirtyEight, jonka käyttämä malli pyrkii huomioimaan mm. joidenkin tutkimuksia tuottavien organisaatioiden taipumuksen systemaattisesti liioitella republikaanien tai demokraattien kannatusta. (Suomessa julkaistaan mielipidemittauksia niin harvakseltaan, ettei niiden aggregoinnista ole kehittynyt omaa journalismin lajiaan kuten esimerkiksi USA:ssa.)

Yllä olevassa kuviossa mielipidemittausten tulokset on yhdistetty kyselyiden vastaajamäärällä painotettuna, ilman muita kertoimia ja laskettu lopuksi uudet virhemarginaalit yhdistetyn vastaajamäärän mukaan. Laskelman perusteella vihreät olisi siis perussuomalaisia suositumpi, joskaan ei aivan yhtä pitkällä kaulalla kuin Ylen kyselyn alkuperäisten lukujen valossa. Tässä kaikkien puolueiden yhdistetyt luvut:

SDP	20,7 %
keskusta	19,9 %
kokoomus	17,3 %
vihreät	12,5 %
PS	10,3 %
vasemmistoliitto	8,2 %
RKP	4,7 %
KD	3,6 %
muut	2,9 %

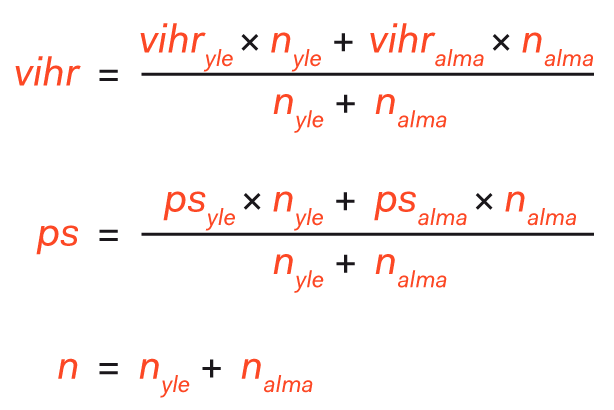
Yhdistämiseen käyttämäni laskukaavat ovat hyvin yksinkertaisia:

jne.

Tällaisia yksinkertaisia kaavoja käyttäen laskelman tekeminen on helppoa, ja vaikka sillä onkin puutteensa verrattuna mielipideaggregaattorien käyttämiin hienostuneempiin malleihin, laskelman tulos kertoo kuitenkin puoluekannatuksesta enemmän kuin yksittäinen mielipidemittaus. Kun tämä ei ole tämän vaikeampaa, ihmettelen kyllä vähän, miksi media ei Suomessa vaikuta yhtään kiinnostuneelta tekemään puoluekannatuslaskelmia jotka perustuisivat useampaan kuin yhteen mielipidemittaukseen!

Virhemarginaali antaa liian ruusuisen kuvan mielipidemittauksen luotettavuudesta

Edellä esitetyissä laskelmissa ja mielipidemittauksen tutkimuksen virhemarginaalista puhuttaessa ylipäänsäkin lähdetään implisiittisesti siitä oletuksesta, että tutkimuksen otos on harhaton (engl. unbiased) tai ainakin, että otoksen mahdollinen vinouma on pystytty jollain tavalla oikaisemaan. Näin harvemmin todellisuudessa on.

Harhattomuus tarkoittaa sitä, että ainut tekijä joka vaikuttaa siihen, kenet populaatiosta poimitaan mielipidemittauksen tutkimusotokseen on sattuma. Jos nostamme erivärisiä palloja sisältävästä valtavasta pussista 1 121 palloa ja niistä 133 on vihreitä, voidaan virhemarginaalin laskentakaavaa käyttäen helposti selvittää, että kaikista pussissa olevista palloista on 95 prosentin todennäköisyydellä vihreitä 11,3–15,3 % (13,3 ± 2,0). Virhemarginaali kuvaa siis otantavirhettä (engl. sampling error), eli sitä, että satunnaisotantaan osuu harvoin aivan täsmälleen populaation sisäistä jakaumaa kuvaava joukko kohteita.

Mielipidemittauksiin vastaavat ihmiset eivät kuitenkaan ole yhtä helppo tutkimuskohde kuin pallot, vaan otantavirheen lisäksi tulosta vääristävät erilaiset otosharhat (engl. sampling bias):

• Tutkimukseen ei ole käytännössä mahdollista poimia satunnaista joukkoa kaikista äänestysikäisistä suomalaisista, vaan otanta joudutaan tekemään esimerkiksi arpomalla haastateltavat numeropalveluun rekisteröityjen puhelinnumeroiden joukosta. Tutkimuksen otantakehikko (engl. sampling frame) on tällöin ne suomalaiset, joilla on julkinen puhelinnumero. Se ei ole täsmälleen sama joukko kuin kaikki äänestysikäiset suomalaiset, mistä johtuen kyselyyn sisältyy peittovirhe (coverage error).

• Osalla suomalaisista on käytössään useampi kuin yksi puhelinnumero, joten heidän valikoitumisensa puhelinnumeroista arpomalla muodostettuun otokseen on keskimääräistä todennäköisempää. Jotkut taas voivat esimerkiksi vuorotyön vuoksi olla tutkimuksentekoaikana huonosti tavoitettavissa puhelimitse, jolloin heidän valikoitumisensa otokseen on vähemmän todennäköistä. Tällaisten syiden vuoksi puhelimitse tehtävään mielipidemittaukseen sisältyy myös valikoitumisharha (engl. selection bias).

• Kaikki tutkimukseen valitut eivät syystä tai toisesta halua vastata kyselyyn. Varsinkin verkkokyselyissä vastauskato on yleensä iso ongelma ja sen aiheuttama vinouma (engl. non-response bias) potentiaalisesti suuri.

Otantavirheen ja erilaisten otosharhojen lisäksi tulosta vääristää vielä vastausharha (engl. response bias), joka on kattotermi erilaisille syille, joiden vuoksi osallistujien antamat vastaukset kyselyyn eivät aina täysin vastaa sitä, miten he todellisuudessa ajattelevat tai toimivat. Kaikki eivät esimerkiksi halua myöntää haastattelijalle kannattavansa rasistiseksi väitettyä puoluetta. Toisaalta haastateltava saattaa vastata eri kysymykseen kuin mikä häneltä on kysytty, esimerkiksi kuntavaalikannatusta koskevassa kyselyssä siihen, mitä puoluetta hän äänestäisi eduskuntavaaleissa.

Otantavirhe aiheuttaa mielipidemittauksen tuloksiin epätarkkuutta, jota voi pienentää otoskokoa kasvattamalla. Vinoutunut otos ja vastausharha sen sijaan vääristävät tuloksia usein tavoilla, joiden korjaaminen ei ole näin yksinkertaista. Jos esimerkiksi jonkin puolueen kannattajissa on enemmän vuorotöissä käyviä kuin muiden, tämän puolueen kannattajista valikoituu otokseen helposti todellista kannatusta pienempi osuus ja tämä vääristää puolueen kannatuslukuja.

Mielipidemittausten tekijät pyrkivät korjaamaan otosharhan aiheuttamaa virhettä esimerkiksi käyttämällä yksinkertaisen satunnaisotannan sijaan ositettua otantaa eli kiintiöpoimintaa (engl. stratified sampling), jolla huolehditaan siitä, että kaikkiin merkittäviin sosioekonomisiin ryhmiin (esim. miehet ja naiset, suomen- ja ruotsinkieliset) kuuluvien määrä otoksessa vastaa heidän osuuttaan väestössä. Tällaisista korjaavista toimista huolimatta mielipidemittausten tuloksiin sisältyy aina ilmoitetun virhemarginaalin lisäksi edellä mainittujen tekijöiden yhteenlasketun vaikutuksen aiheuttama metodologinen virhemarginaali. Termin kehittäjä Nate Silver arvioi yhdysvaltalaisissa mielipidemittauksissa sen olevan tavallisesti samaa suuruusluokkaa kuin tavallisen otantavirhemarginaalinkin. Tämä tarkoittaa, että karkeasti arvioiden yksittäisen mielipidemittauksen todellinen virhemarginaali voi olla kaksinkertainen ilmoitettuun nähden.

Tarinan opetus

Mielipidemittausten tuloksiin sisältyy runsaasti epävarmuutta. Todellinen virhemarginaali voi metodologiset tekijät huomioonottaen isoimpien puolueiden osalta olla kaksinkertainen tutkimuksen tekijän ilmoittamaan verrattuna ja osa todellisista kannatusluvuista voi löytyä jopa tämän laajemman virhemarginaalin ulkopuolelta. Niinpä reilusti virhemarginaalin sisään mahtuvat muutokset puolueiden kannatuksessa tai erot niiden keskinäisessä suosiossa ovat todennäköisemmin sattuman aiheuttamaa kuin merkki mistään todellisesta ilmiöstä, eikä niillä ole juurikaan uutisarvoa. Parempi käsitys puolueiden kannatuksesta saadaan, kun useampien mielipidemittausten tulokset yhdistetään.

Maarten Lambrechtsin mainio Rock ’n Poll -sivusto auttaa hahmottamaan, miten paljon otantavirhe vaikuttaa mielipidemittausten tuloksiin. Jokaisen politiikan toimittajan kannattaisi vilkaista sitä ennen kuin kirjoittaa uutisena, miten jonkin puolueen kannatus on muuttunut 0,4 prosenttiyksikköä edellisestä vertailusta.